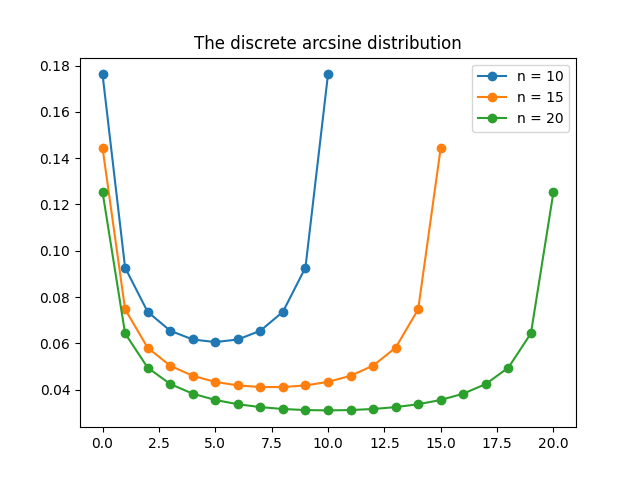
The discrete arcsine distribution is a probability distribution on \(\{0,1,\ldots,n\}\). It is a u-shaped distribution. There are peaks at \(0\) and \(n\) and a dip in the middle. The figure below shows the probability distribution function for \(n=10,15, 20\).
The probability distribution function of the arcsine distribution is given by
\(\displaystyle{p_n(k) = \frac{1}{2^{2n}}\binom{2k}{k}\binom{2n-2k)}{n-k}\text{ for } k \in \{0,1,\ldots,n\}}\)
The discrete arcsine distribution is related to simple random walks and to an interesting Markov chain called the Burnside process. The connection with simple random walks is explained in Chapter 3, Volume 1 of An Introduction to Probability and its applications by William Feller. The connection to the Burnside process was discovered by Persi Diaconis in Analysis of a Bose-Einstein Markov Chain.
The discrete arcsine distribution gets its name from the continuous arcsine distribution. Suppose \(X_n\) is distributed according to the discrete arcsine distribution with parameter \(n\). Then the normalized random variables \(X_n/n\) converges in distribution to the continuous arcsine distribution on \([0,1]\). The continuous arcsine distribution has the probability density function
\(\displaystyle{f(x) = \frac{1}{\pi\sqrt{x(1-x)}} \text{ for } 0 \le x \le 1}\)
This means that continuous arcsine distribution is a beta distribution with \(\alpha=\beta=1/2\). It is called the arcsine distribution because the cumulative distribution function involves the arcsine function
\(\displaystyle{F(x) = \int_0^x f(y)dy = \frac{2}{\pi}\arcsin(\sqrt{x}) \text{ for } 0 \le x \le 1}\)
There is another connection between the discrete and continuous arcsine distributions. The continuous arcsine distribution can be used to sample the discrete arcsine distribution. The two step procedure below produces a sample from the discrete arcsine distribution with parameter \(n\):
- Sample \(p\) from the continuous arcsine distribution.
- Sample \(X\) from the binomial distribution with parameters \(n\) and \(p\).
This means that the discrete arcsine distribution is actually the beta-binomial distribution with parameters \(\alpha = \beta =1/2\). I was surprised when I was told this, and couldn’t find a reference. The rest of this blog post proves that the discrete arcsine distribution is an instance of the beta-binomial distribution.
As I showed in this post, the beta-binomial distribution has probability distribution function:
\(\displaystyle{q_{\alpha,\beta,n}(k) = \binom{n}{k}\frac{B(k+\alpha, n-k+\alpha)}{B(a,b)}},\)
where \(B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}\) is the Beta-function. To show that the discrete arc sine distribution is an instance of the beta-binomial distribution we need that \(p_n(k)=q_{1/2,1/2,n}(k)\). That is
\(\displaystyle{ \binom{n}{k}\frac{B(k+1/2, n-k+1/2)}{B(1/2,1/2)} = \frac{1}{2^{2n}}\binom{2k}{k}\binom{2n-2k}{n-k}}\),
for all \(k = 0,1,\ldots,n\). To prove the above equation, we can first do some simplifying to \(q_{1/2,1/2,n}(k)\). By definition
\(\displaystyle{\frac{B(k+1/2, n-k+1/2)}{B(1/2,1/2)} = \frac{\frac{\Gamma(k+1/2)\Gamma(n-k+1/2)}{\Gamma(n+1)}}{\frac{\Gamma(1/2)\Gamma(1/2)}{\Gamma(1)}} = \frac{1}{n!}\frac{\Gamma(k+1/2)}{\Gamma(1/2)}\frac{\Gamma(n-k+1/2)}{\Gamma(1/2)}}\),
where I have used that \(\Gamma(m)=(m-1)!\) factorial if \(m\) is a natural number. The Gamma function \(\Gamma(x)\) also satisfies the property \(\Gamma(x+1)=x\Gamma(x)\). Using this repeatedly gives
\(\displaystyle{\Gamma(k+1/2) = (k-1/2) \times (k-3/2) \times \cdots \times \frac{3}{2}\times\frac{1}{2}\times\Gamma(1/2) }. \)
This means that
\(\displaystyle{\frac{\Gamma(k+1/2)}{\Gamma(1/2)} = (k-1/2) \times (k-3/2) \times \cdots \times \frac{3}{2}\times\frac{1}{2} = \frac{(2k-1)\times(2k-3)\times \cdots \times 3 \times 1}{2^k}=\frac{(2k-1)!!}{2^k}},\)
where \((2k-1)!!=(2k-1)\times (2k-3)\times\cdots \times 3 \times 1\) is the double factorial. The same reasoning gives
\(\displaystyle{\frac{\Gamma(n-k+1/2)}{\Gamma(1/2)} =\frac{(2n-2k-1)!!}{2^{n-k}}}.\)
And so
\(\displaystyle{q_{1/2,1/2,n}(k) =\frac{1}{2^nk!(n-k)!}(2k-1)!!(2n-2k-1)!!}.\)
We’ll now show that \(p_n(k)\) is also equal to the above final expression. Recall
\(\displaystyle{p_n(k) = \frac{1}{2^{2n}} \binom{2k}{k}\binom{2(n-k)}{n-k} = \frac{1}{2^{2n}}\frac{(2k)!(2(n-k))!}{k!k!(n-k)!(n-k)!} = \frac{1}{2^nk!(n-k)!}\frac{(2k)!}{k!2^k}\frac{(2n-2k)!}{(n-k)!2^{n-k}}}.\)
And so it suffices to show \(\frac{(2k)!}{k!2^k} = (2k-1)!!\) (and hence \(\frac{(2n-2k)!}{(n-k)!2^{n-k}}=(2n-2k-1)!!\)). To see why this last claim holds, note that
\(\displaystyle{\frac{(2k)!}{k!2^k} = \frac{(2k)\times (2k-1)\times(2k-2)\times\cdots\times 3 \times 2 \times 1}{(2k)\times (2k-2)\times \cdots \times 2} = (2k-1)!!}\)
Showing that \(p_{n}(k)=q_{n,1/2,1/2}(k)\) as claimed.