random-matrices – mathstoshare

An \(n \times n\) matrix \(M \in \mathbb{R}^{n \times n}\) is orthogonal if \(M^\top M = I\). The set of all \(n \times n\) orthogonal matrices is a compact group written as \(O_n\). The uniform distribution on \(O_n\) is called Haar measure. There are many ways to generate random matrices for Haar measure. One of which is based on the Gram-Schmidt algorithm.

Proposition. Let \(X\) be a \(n \times n\) matrix such that each entry \(X_{ij}\) is an independent standard normal random variable. Let \(x_1,x_2,\ldots,x_n \in \mathbb{R}^n\) be the columns of \(X\) and let \(q_1,q_2,\ldots,q_n \in \mathbb{R}^n\) be the result of applying Gram-Schmidt to \(x_1,x_2,\ldots,x_n\). Then the matrix \(M=[q_1,q_2,\ldots,q_n] \in O_n\) is distributed according to Haar measure.

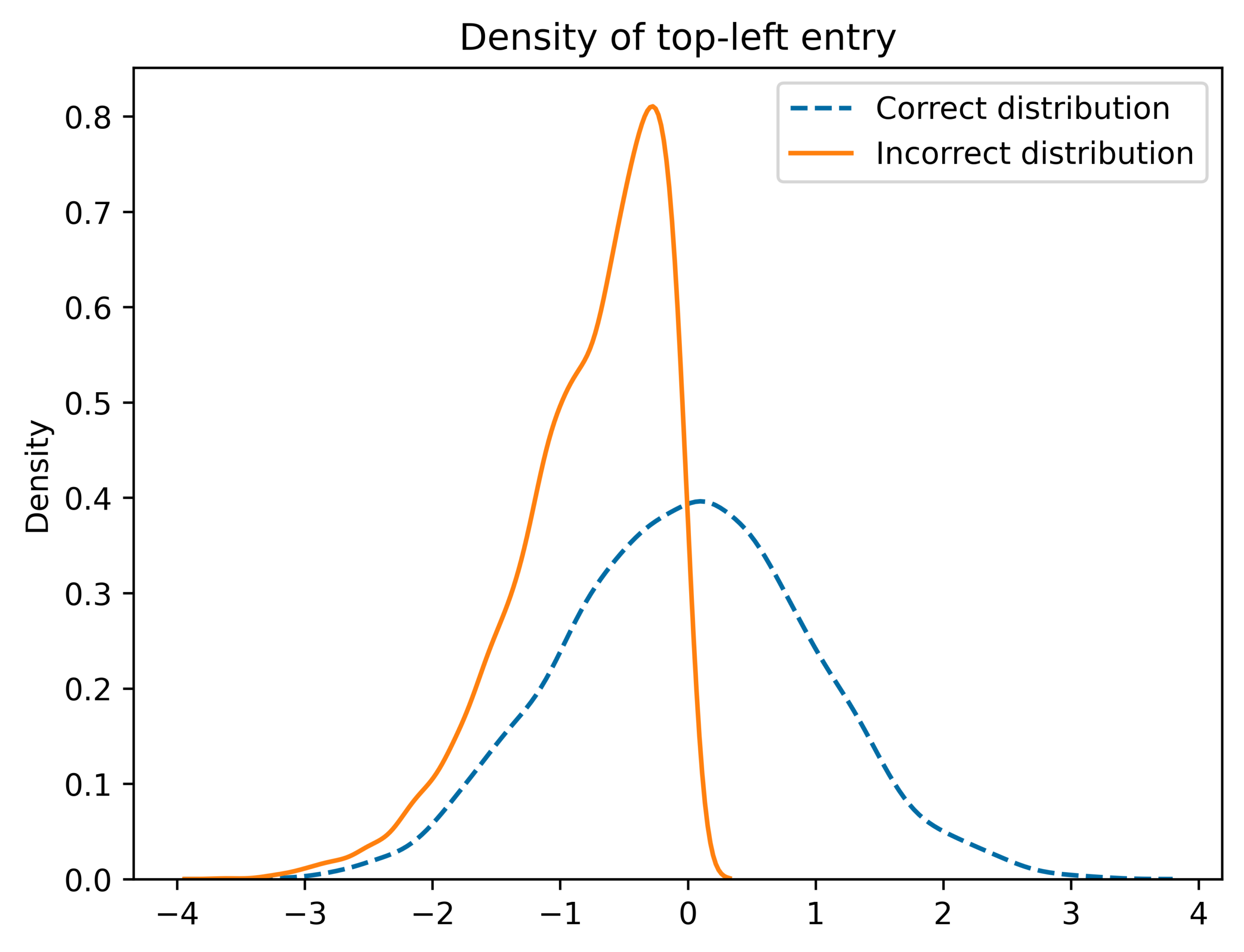
Another way of stating the above proposition is that if \(X\) has i.i.d. standard normal entries, and \(Q,R\) is a QR-factorization of \(X\) calculated using Gram-Schmidt, then \(Q \in O_n\) is distributed according to Haar measure. However, most numerical libraries do not use Gram-Schmidt to calculate the QR-factorization of a matrix. This means that if you generate a random \(X\) and then use your computer’s QR-factorization function, then the result might not be Haar distributed as the plot below shows.

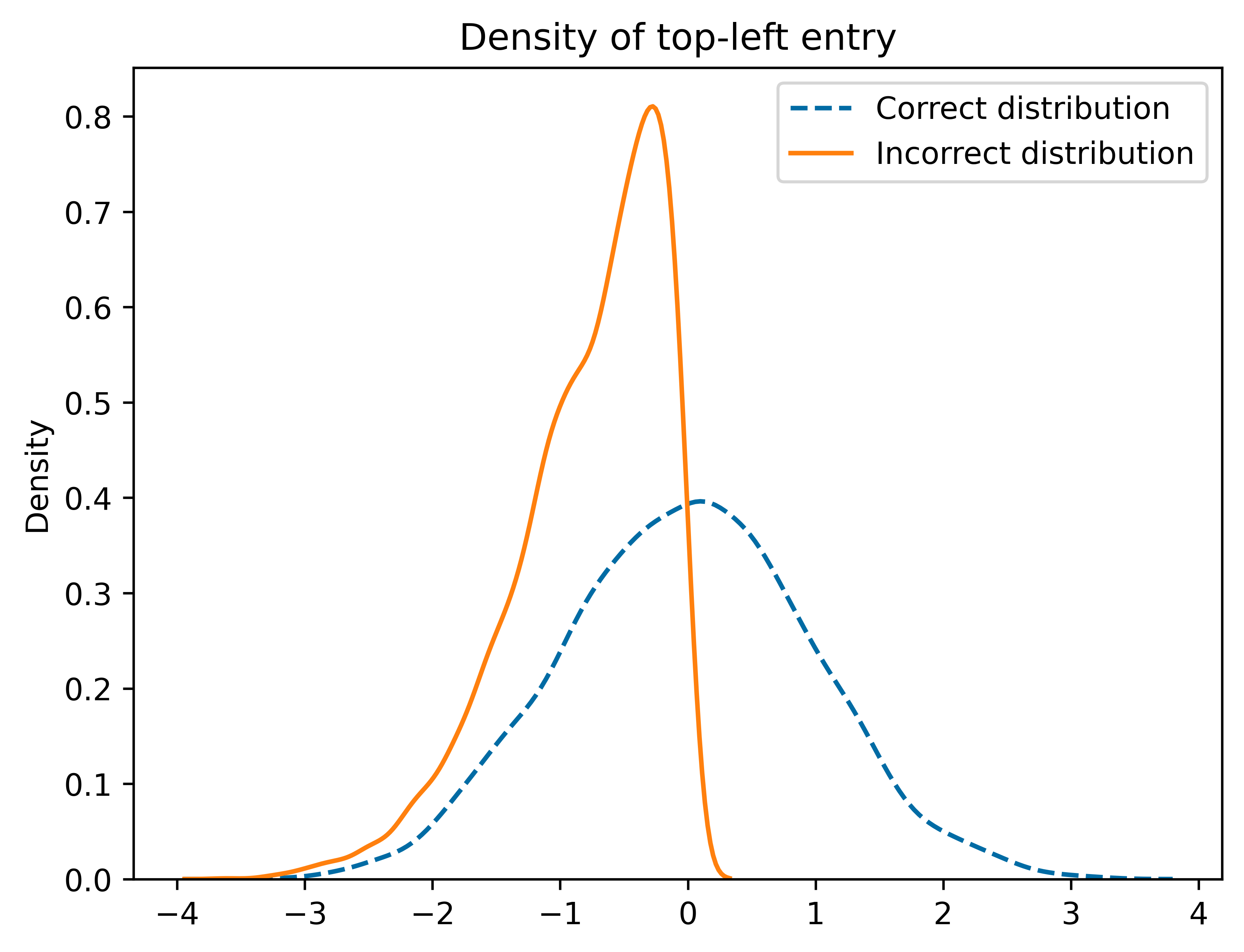
The plot shows an estimate of the distribution of \(\sqrt{n}M_{11}\), the top-left entry of a matrix \(M\). When \(M\) is correctly sampled, the distribution is symmetric about 0. When \(M\) is incorrectly sampled the distribution is clearly biased towards negative numbers.

Fortunately there is a fix described in [1]! We can first use any QR-factorization algorithm to produce \(Q,R\) with \(X=QR\). We then compute a diagonal matrix \(L\) with \(L_{ii} = \mathrm{Sign}(R_{ii})\). Then, the matrix \(M=QL\) is Haar distributed. The following python code thus samples a Haar distributed matrix in \(O_n\).

import numpy as np

def sample_M(n):
    M = np.random.randn(n, n)
    Q, R = np.linalg.qr(M)
    L = np.sign(np.diag(R))
    return Q*L[None,:]

References

[1] Mezzadri, Francesco. “How to generate random matrices from the classical compact groups.” arXiv preprint math-ph/0609050 (2006). https://arxiv.org/abs/math-ph/0609050

I recently gave a talk at the Stanford student probability seminar on Haar distributed random matrices. My notes and many further references are available here.

Tag: random-matrices

Uniformly sampling orthogonal matrices

References