mathstoshare

Tag: machine-learning

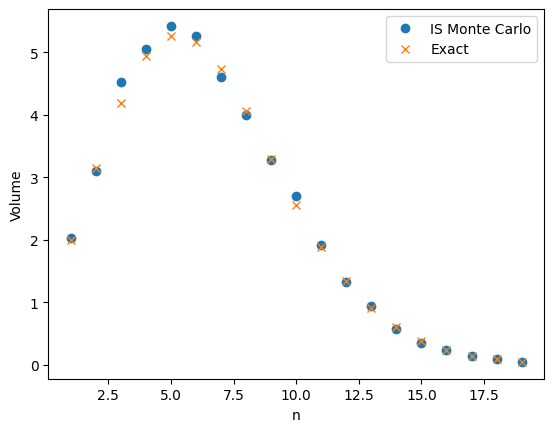
  • The sample size required for importance sampling

    My last post was about using importance sampling to estimate the volume of high-dimensional ball. The two figures below compare plain Monte Carlo to using importance sampling with a Gaussian proposal. Both plots use \(M=1,000\) samples to estimate \(v_n\), the volume of an \(n\)-dimensional ball

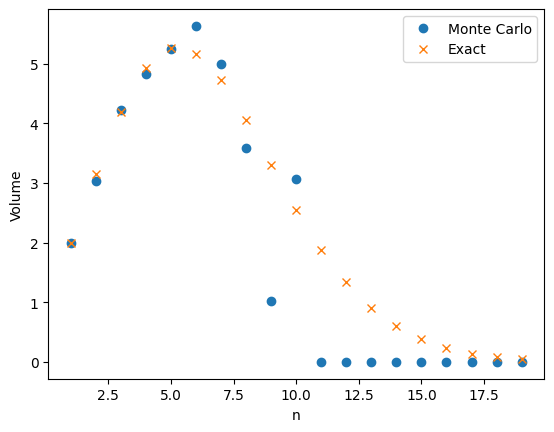
    A friend of mine pointed out that the relative error does not seem to increase with the dimension \(n\). He thought it was too good to be true. It turns out he was right and the relative error does increase with dimension but it increases very slowly. To estimate \(v_n\) the number of samples needs to grow on the order of \(\sqrt{n}\).

    To prove this, we will use the paper The sample size required for importance sampling by Chatterjee and Diaconis [1]. This paper shows that the sample size for importance sampling is determined by the Kullback-Liebler divergence. The relevant result from their paper is Theorem 1.3. This theorem is about the relative error in using importance sampling to estimate a probability.

    In our setting the proposal distribution is \(Q=\mathcal{N}(0,\frac{1}{n}I_n)\). That is the distribution \(Q\) is an \(n\)-dimensional Gaussian vector with mean \(0\) and covariance \(\frac{1}{n}I_n\). The conditional target distribution is \(P\) the uniform distribution on the \(n\) dimensional ball. Theorem 1.3 in [1] tells us how many samples are needed to estimate \(v_n\). Informally, the required sample size is \(M = O(\exp(D(P \Vert Q)))\). Here \(D(P\Vert Q)\) is the Kullback-Liebler divergence between \(P\) and \(Q\).

    To use this theorem we need to compute \(D(P \Vert Q)\). Kullback-Liebler divergence is defined as integral. Specifically

    \(\displaystyle{D(P\Vert Q) = \int_{\mathbb{R}^n} \log\frac{P(x)}{Q(x)}P(x)dx}\)

    Computing the high-dimensional integral above looks challenging. Fortunately, it can reduced to a one-dimensional integral. This is because both the distributions \(P\) and \(Q\) are rotationally symmetric. To use this, define \(P_r,Q_r\) to be the distribution of the norm squared under \(P\) and \(Q\). That is if \(X \sim P\), then \(\Vert X \Vert_2^2 \sim P_R\) and likewise for \(Q_R\). By the rotational symmetry of \(P\) and \(Q\) we have

    \(D(P\Vert Q) = D(P_R \Vert Q_R).\)

    We can work out both \(P_R\) and \(Q_R\). The distribution \(P\) is the uniform distribution on the \(n\)-dimensional ball. And so for \(X \sim P\) and any \(r \in [0,1]\)

    \(\mathbb{P}(\Vert X \Vert_2^2 \le r) = \frac{v_n r^n}{v_n} = r^n.\)

    Which implies that \(P_R\) has density \(P_R(r)=nr^{n-1}\). This means that \(P_R\) is a Beta distribution with parameters \(\alpha = n, \beta = 1\). The distribution \(Q\) is a multivariate Gaussian distribution with mean \(0\) and variance \(\frac{1}{n}I_n\). This means that if \(X \sim Q\), then \(\Vert X \Vert_2^2 = \sum_{i=1}^n X_i^2\) is a scaled chi-squared variable. The shape parameter of \(Q_R\) is \(n\) and scale parameter is \(1/n\). The density for \(Q_R\) is therefor

    \(Q_R(r) = \frac{n^{n/2}}{2^{n/2}\Gamma(n/2)}r^{n/2-1}e^{-nx/2}\)

    The Kullback-Leibler divergence between \(P\) and \(Q\) is therefor

    \(\displaystyle{D(P\Vert Q)=D(P_R\Vert Q_R) = \int_0^1 \log \frac{P_R(r)}{Q_R(r)} P_R(r)dr}\)

    Getting Mathematica to do the above integral gives

    \(D(P \Vert Q) = -\frac{1+2n}{2+2n} + \frac{n}{2}\log(2 e) – (1-\frac{n}{2})\log n + \log \Gamma(\frac{n}{2}).\)

    Using the approximation \(\log \Gamma(z) \approx (z-\frac{1}{2})\log(z)-z+O(1)\) we get that for large \(n\)

    \(D(P \Vert Q) = \frac{1}{2}\log n + O(1)\).

    And so the required number of samples is \(O(\exp(D(P \Vert Q)) = O(\sqrt{n}).\)

    [1] Chatterjee, Sourav, and Persi Diaconis. “THE SAMPLE SIZE REQUIRED IN IMPORTANCE SAMPLING.” The Annals of Applied Probability 28, no. 2 (2018): 1099–1135. https://www.jstor.org/stable/26542331. (Public preprint here https://arxiv.org/abs/1511.01437)

  • Auxiliary variables sampler

    The auxiliary variables sampler is a general Markov chain Monte Carlo (MCMC) technique for sampling from probability distributions with unknown normalizing constants [1, Section 3.1]. Specifically, suppose we have \(n\) functions \(f_i : \mathcal{X} \to (0,\infty)\) and we want to sample from the probability distribution \(P(x) \propto \prod_{i=1}^n f_i(x).\) That is

    \(\displaystyle{ P(x) = \frac{1}{Z}\prod_{i=1}^n f_i(x)},\)

    where \(Z = \sum_{x \in \mathcal{X}} \prod_{i=1}^n f_i(x)\) is a normalizing constant. If the set \(\mathcal{X}\) is very large, then it may be difficult to compute \(Z\) or sample from \(P(x)\). To approximately sample from \(P(x)\) we can run an ergodic Markov chain with \(P(x)\) as a stationary distribution. Adding auxiliary variables is one way to create such a Markov chain. For each \(i \in \{1,\ldots,n\}\), we add a auxiliary variable \(U_i \ge 0\) such that

    \(\displaystyle{P(U \mid X) = \prod_{i=1}^n \mathrm{Unif}[0,f_i(X)]}.\)

    That is, conditional on \(X\), the auxiliary variables \(U_1,\ldots,U_n\) are independent and \(U_i\) is uniformly distributed on the interval \([0,f_i(X)]\). If \(X\) is distributed according to \(P\) and \(U_1,\ldots,U_n\) have the above auxiliary variable distribution, then

    \(\displaystyle{P(X,U) =P(X)P(U\mid X)\propto \prod_{i=1}^n f_i(X) \frac{1}{f_i(X)} I[U_i \le f(X_i)] = \prod_{i=1}^n I[U_i \le f(X_i)]}.\)

    This means that the joint distribution of \((X,U)\) is uniform on the set

    \(\widetilde{\mathcal{X}} = \{(x,u) \in \mathcal{X} \times (0,\infty)^n : u_i \le f(x_i) \text{ for all } i\}.\)

    Put another way, suppose we could jointly sample \((X,U)\) from the uniform distribution on \(\widetilde{\mathcal{X}}\). Then, the above calculation shows that if we discard \(U\) and only keep \(X\), then \(X\) will be sampled from our target distribution \(P\).

    The auxiliary variables sampler approximately samples from the uniform distribution on \(\widetilde{\mathcal{X}}\) is by using a Gibbs sampler. The Gibbs samplers alternates between sampling \(U’\) from \(P(U \mid X)\) and then sampling \(X’\) from \(P(X \mid U’)\). Since the joint distribution of \((X,U)\) is uniform on \(\widetilde{\mathcal{X}}\), the conditional distributions \(P(X \mid U)\) and \(P(U \mid X)\) are also uniform. The auxiliary variables sampler thus transitions from \(X\) to \(X’\) according to the two step process

    1. Independently sample \(U_i\) uniformly from \([0,f_i(X)]\).
    2. Sample \(X’\) uniformly from the set \(\{x \in \mathcal{X} : f_i(x) \ge u_i \text{ for all } i\}\).

    Since the auxiliary variables sampler is based on a Gibbs sampler, we know that the joint distribution of \((X,U)\) will converge to the uniform distribution on \(\mathcal{X}\). So when we discard \(U\), the distribution of \(X\) will converge to the target distribution \(P\)!

    Auxiliary variables in practice

    To perform step 2 of the auxiliary variables sampler we have to be able to sample uniformly from the sets

    \(\mathcal{X}_u = \{x \in \mathcal{X}:f_i(x) \ge u_i \text{ for all } i\}. \)

    Depending on the nature of the set \(\mathcal{X}\) and the functions \(f_i\), it might be difficult to do this. Fortunately, there are some notable examples where this step has been worked out. The very first example of auxiliary variables is the Swendsen-Wang algorithm for sampling from the Ising model [2]. In this model it is possible to sample uniformly from \(\mathcal{X}_u\). Another setting where we can sample exactly is when \(\mathcal{X}\) is the real numbers \(\mathcal{R}\) and each \(f_i\) is an increasing function of \(x\). This is explored in [3] where they apply auxiliary variables to sampling from Bayesian posteriors.

    There is an alternative to sampling exactly from the uniform distribution on \(\mathcal{X}_u\). Instead of sampling \(X’\) uniformly from \(\mathcal{X}_u\), we can run a Markov chain from the old \(X\) that has the uniform distribution as a stationary distribution. This approach leads to another special case of auxiliary variables which is called “slice sampling” [4].

    References

    [1] Andersen HC, Diaconis P. Hit and run as a unifying device. Journal de la societe francaise de statistique & revue de statistique appliquee. 2007;148(4):5-28. http://www.numdam.org/item/JSFS_2007__148_4_5_0/
    [2] Swendsen RH, Wang JS. Nonuniversal critical dynamics in Monte Carlo simulations. Physical review letters. 1987 Jan 12;58(2):86. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.58.86
    [3] Damlen P, Wakefield J, Walker S. Gibbs sampling for Bayesian non‐conjugate and hierarchical models by using auxiliary variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology). 1999 Apr;61(2):331-44. https://rss.onlinelibrary.wiley.com/doi/abs/10.1111/1467-9868.00179
    [4] Neal RM. Slice sampling. The annals of statistics. 2003 Jun;31(3):705-67. https://projecteuclid.org/journals/annals-of-statistics/volume-31/issue-3/Slice-sampling/10.1214/aos/1056562461.full

  • Log-sum-exp trick with negative numbers

    Suppose you want to calculate an expression of the form

    \(\displaystyle{\log\left(\sum_{i=1}^n \exp(a_i) – \sum_{j=1}^m \exp(b_j)\right)},\)

    where \(\sum_{i=1}^n \exp(a_i) > \sum_{j=1}^m \exp(b_j)\). Such expressions can be difficult to evaluate directly since the exponentials can easily cause overflow errors. In this post, I’ll talk about a clever way to avoid such errors.

    If there were no terms in the second sum we could use the log-sum-exp trick. That is, to calculate

    \(\displaystyle{\log\left(\sum_{i=1}^n \exp(a_i) \right)},\)

    we set \(a=\max\{a_i : 1 \le i \le n\}\) and use the identity

    \(\displaystyle{a + \log\left(\sum_{i=1}^n \exp(a_i-a)\right) = \log\left(\sum_{i=1}^n \exp(a_i)\right)}. \)

    Since \(a_i \le a\) for all \(i =1,\ldots,n\), the left hand side of the above equation can be computed without the risk of overflow. To calculate,

    \(\displaystyle{\log\left(\sum_{i=1}^n \exp(a_i) – \sum_{j=1}^m \exp(b_j)\right)},\)

    we can use the above method to separately calculate

    \(\displaystyle{A = \log\left(\sum_{i=1}^n \exp(a_i) \right)}\) and \(\displaystyle{B = \log\left(\sum_{j=1}^m \exp(b_j)\right)}.\)

    The final result we want is

    \(\displaystyle{\log\left(\sum_{i=1}^n \exp(a_i) – \sum_{j=1}^m \exp(b_j) \right) = \log(\exp(A) – \exp(B)) = A + \log(1-\exp(B-A))}.\)

    Since $A > B$, the right hand side of the above expression can be evaluated safely and we will have our final answer.

    R code

    The R code below defines a function that performs the above procedure

    # Safely compute log(sum(exp(pos)) - sum(exp(neg)))
# The default value for neg is an empty vector.

logSumExp <- function(pos, neg = c()){
  max_pos <- max(pos)
  A <- max_pos + log(sum(exp(pos - max_pos)))
  
  # If neg is empty, the calculation is done
  if (length(neg) == 0){
    return(A)
  }
  
  # If neg is non-empty, calculate B.
  max_neg <- max(neg)
  B <- max_neg + log(sum(exp(neg - max_neg)))
  
  # Check that A is bigger than B
  if (A <= B) {
    stop("sum(exp(pos)) must be larger than sum(exp(neg))")
  }
  
  # log1p() is a built in function that accurately calculates log(1+x) for |x| << 1
  return(A + log1p(-exp(B - A)))
}

    An example

    The above procedure can be used to evaulate

    \(\displaystyle{\log\left(\sum_{i=1}^{200} i! – \sum_{i=1}^{500} \binom{500}{i}^2\right)}.\)

    Evaluating this directly would quickly lead to errors since R (and most other programming languages) cannot compute \(200!\). However, R has the functions lfactorial() and lchoose() which can compute \(\log(i!)\) and \(\log\binom{n}{i}\) for large values of \(i\) and \(n\). We can thus put this expression in the general form at the start of this post

    \(\displaystyle{\log\left(\sum_{i=1}^{200} \exp(\log(i!)) – \sum_{i=1}^{500} \exp\left(2\log\binom{500}{i}\right)\right)}.\)

    The following R code thus us exactly what we want:

    pos <- sapply(1:200, lfactorial)
neg <- sapply(1:500, function(i){2*lchoose(500, i)})

logSumExp(pos, neg)
# 863.237

  • [Link Post] Complexity Penalties in Statistical Machine Learning

    Earlier in the year I wrote a post on Less Wrong about some of the material I learnt at the 2019 AMSI Summer School. You can read it here. On a related note, applications are open for the 2020 AMSI Summer School at La Trobe University. I highly recommend attending!