-
Poisson approximations to the negative binomial distribution
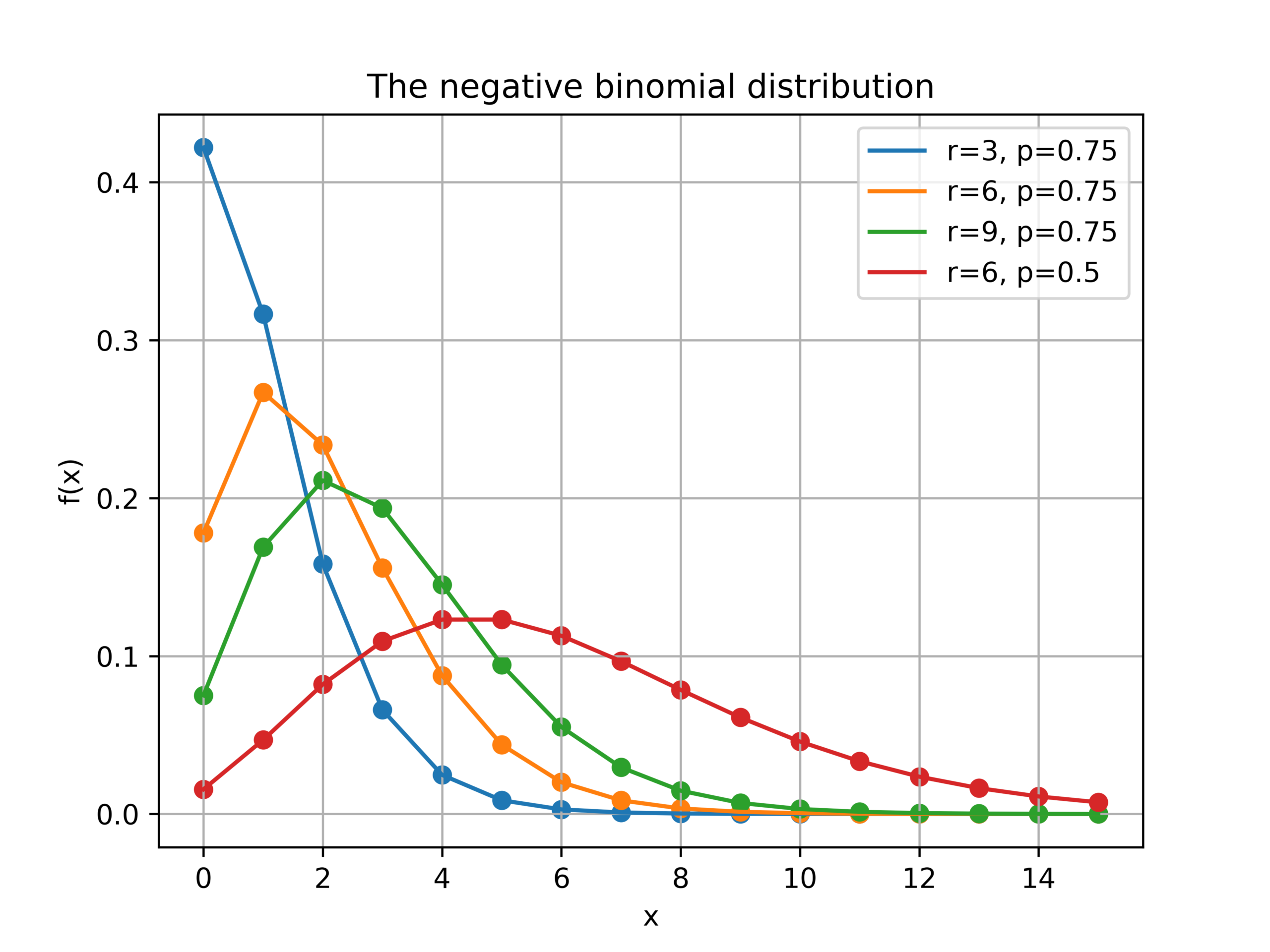
This post is an introduction to the negative binomial distribution and a discussion of different ways of approximating the negative binomial distribution. The negative binomial distribution describes the number of times a coin lands on tails before…
-
Jigsaw puzzles and the isoperimetric inequality

The 2025 World Jigsaw Puzzle Championship recently took place in Spain. In the individual heats, competitors had to choose their puzzle. Each competitor could either complete a 500-piece rectangular puzzle or a 500-piece circular puzzle. For example,…
-
The Multivariate Hypergeometric Distribution
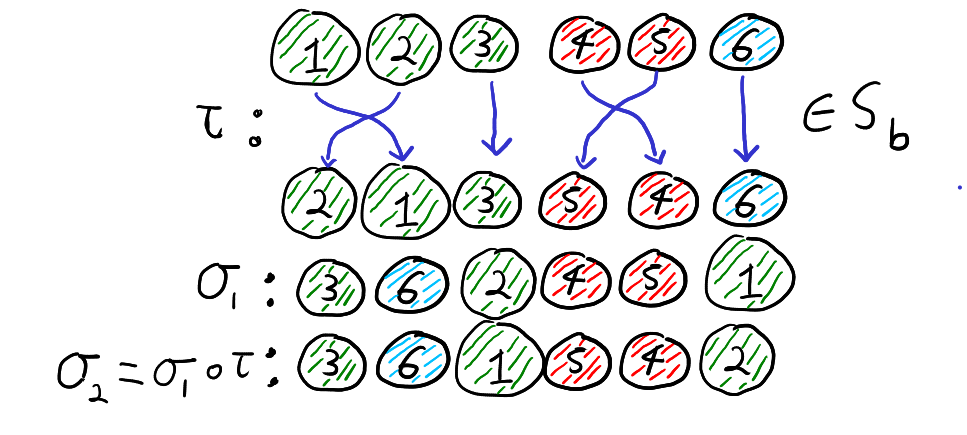
The hypergeometric distribution describes the number of white balls in a sample of \(n\) balls draw without replacement from an urn with \(m_W\) white balls and \(m_B\) black balls. The probability of having \(x\) white balls in…
-
The maximum of geometric random variables
I was working on a problem involving the maximum of a collection of geometric random variables. To state the problem, let \((X_i)_{i=1}^n\) be i.i.d. geometric random variables with success probability \(p=p(n)\). Next, define \(M_n = \max\{X_i :…
-
“Uniformly random”

The term “uniformly random” sounds like a contradiction. How can the word “uniform” be used to describe anything that’s random? Uniformly random actually has a precise meaning, and, in a sense, means “as random as possible.” I’ll…
-
Understanding the Ratio of Uniforms Distribution
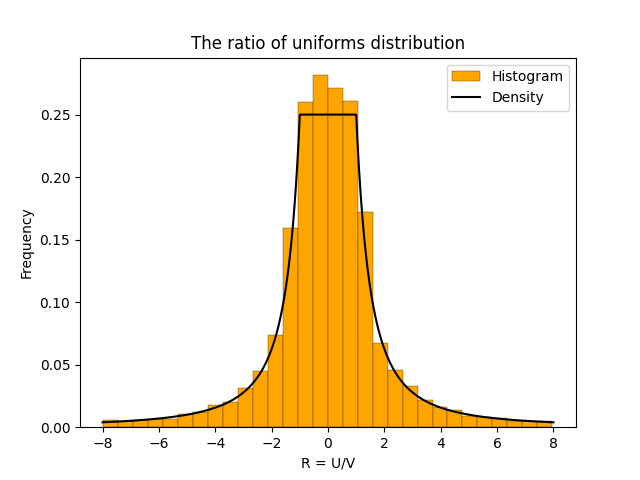
The ratio of uniforms distribution is used in rejection sampling. The density of the distribution has a table mountain shape. In this post the density is derived geometrically.
-
The discrete arcsine distribution
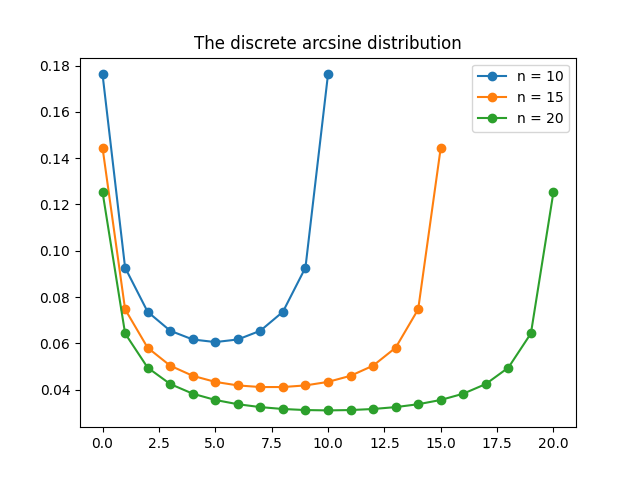
The discrete arcsine distribution is an interesting distribution with connections to random walks, Markov chains and the Beta distribution. This post shows that the discrete arcsine distribution is a special case of the beta-binomial distribution.
-
The sample size required for importance sampling
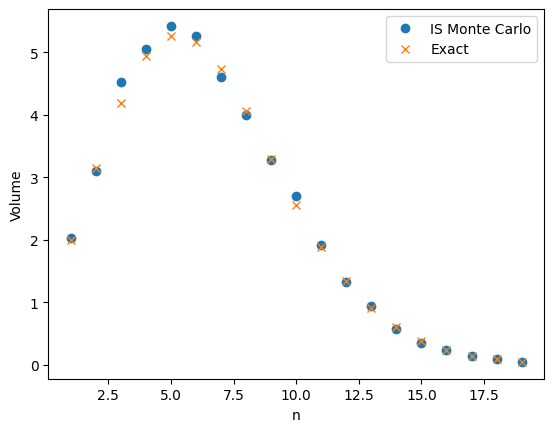
My last post was about using importance sampling to estimate the volume of high-dimensional ball. The two figures below compare plain Monte Carlo to using importance sampling with a Gaussian proposal. Both plots use \(M=1,000\) samples to…
-
Monte Carlo integration in high dimensions
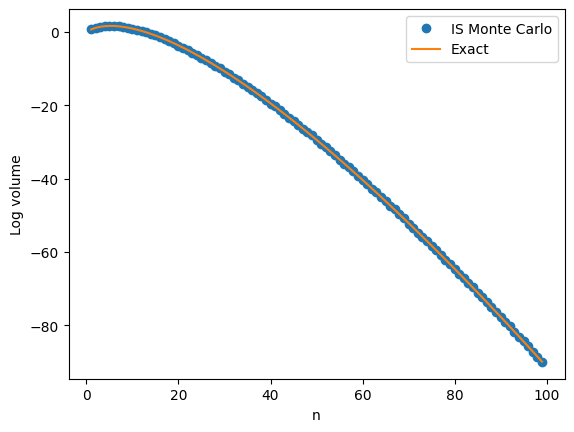
Plain Monte Carlo often fails in high dimensional problems such as estimating the volume of a high dimensional ball. Importance sampling is a powerful variance reduction tool.
-
Uniformly sampling orthogonal matrices
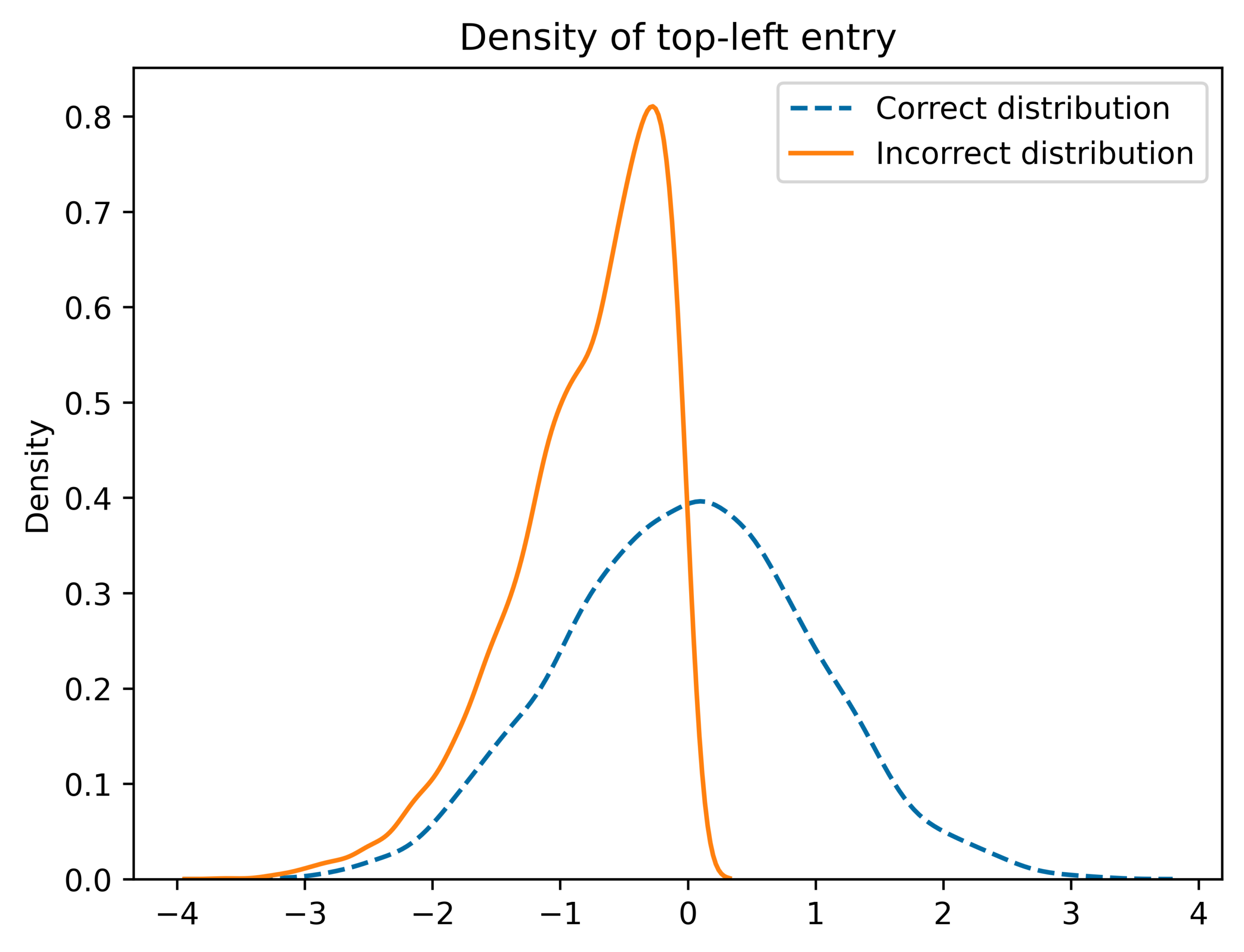
An \(n \times n\) matrix \(M \in \mathbb{R}^{n \times n}\) is orthogonal if \(M^\top M = I\). The set of all \(n \times n\) orthogonal matrices is a compact group written as \(O_n\). The uniform distribution on…
-
Auxiliary variables sampler
The auxiliary variables sampler is a general Markov chain Monte Carlo (MCMC) technique for sampling from probability distributions with unknown normalizing constants [1, Section 3.1]. Specifically, suppose we have \(n\) functions \(f_i : \mathcal{X} \to (0,\infty)\) and…
-
Fibonacci series
In “Probabilizing Fibonacci Numbers” Persi Diaconis recalls asking Ron Graham to help him make his undergraduate number theory class more fun. Persi asks about the chance a Fibonacci number is even and whether infinitely many Fibonacci numbers…
-
The fast Fourier transform as a matrix factorization
The discrete Fourier transform (DFT) is a mapping from \(\mathbb{C}^n\) to \(\mathbb{C}^n\). Given a vector \(u \in \mathbb{C}^n\), the discrete Fourier transform of \(u\) is another vector \(U \in \mathbb{C}^n\) given by, \(\displaystyle{U_k = \sum_{j=0}^{n-1} \exp\left(-2 \pi…
-
Doing Calvin’s homework
Growing up, my siblings and I would read a lot of Bill Watterson’s Calvin and Hobbes. I have fond memories of spending hours reading and re-reading our grandparents collection during the school holidays. The comic strip is…
-
Bernoulli’s inequality and probability
Suppose we have independent events \(E_1,E_2,\ldots,E_m\), each of which occur with probability \(1-\varepsilon\). The event that all of the \(E_i\) occur is \(E = \bigcap_{i=1}^m E_i\). By using independence we can calculate the probability of \(E\), \(P(E)…
-
Solving a system of equations vs inverting a matrix
I used to have trouble understanding why inverting an \(n \times n\) matrix required the same order of operations as solving an \(n \times n\) system of linear equations. Specifically, if \(A\) is an \(n\times n\) invertible…
-
Braids and the Yang-Baxter equation
I recently gave a talk on the Yang-Baxter equation. The focus of the talk was to state the connection between the Yang-Baxter equation and the braid relation. This connection comes from a system of interacting particles. In…
-
Concavity of the squared sum of square roots
The \(p\)-norm of a vector \(x\in \mathbb{R}^n\) is defined to be: \(\displaystyle{\Vert x \Vert_p = \left(\sum_{i=1}^n |x_i|^p\right)^{1/p}}.\) If \(p \ge 1\), then the \(p\)-norm is convex. When \(0<p<1\), this function is not convex and actually concave when…
-
Log-sum-exp trick with negative numbers
Suppose you want to calculate an expression of the form \(\displaystyle{\log\left(\sum_{i=1}^n \exp(a_i) – \sum_{j=1}^m \exp(b_j)\right)},\) where \(\sum_{i=1}^n \exp(a_i) > \sum_{j=1}^m \exp(b_j)\). Such expressions can be difficult to evaluate directly since the exponentials can easily cause overflow errors.…
-
The beta-binomial distribution
The beta-binomial model is a Bayesian model used to analyze rates. For a great derivation and explanation of this model, I highly recommend watching the second lecture from Richard McElreath’s course Statistical Rethinking. In this model, the…
-
Two sample tests as correlation tests
Suppose we have two samples \(Y_1^{(0)}, Y_2^{(0)},\ldots, Y_{n_0}^{(0)}\) and \(Y_1^{(1)},Y_2^{(1)},\ldots, Y_{n_1}^{(1)}\) and we want to test if they are from the same distribution. Many popular tests can be reinterpreted as correlation tests by pooling the two samples…
-
MCMC for hypothesis testing
A Monte Carlo significance test of the null hypothesis \(X_0 \sim H\) requires creating independent samples \(X_1,\ldots,X_B \sim H\). The idea is if \(X_0 \sim H\) and independently \(X_1,\ldots,X_B\) are i.i.d. from \(H\), then for any test…
-
How to Bake Pi, Sherman-Morrison and log-sum-exp
A few months ago, I had the pleasure of reading Eugenia Cheng‘s book How to Bake Pi. Each chapter starts with a recipe which Cheng links to the mathematical concepts contained in the chapter. The book is…
-
Looking back on the blog
Next week I’ll be starting the second year of my statistics PhD. I’ve learnt a lot from taking the first year classes and studying for the qualifying exams. Some of what I’ve learnt has given me a…
-
Total Variation and Marathon Running
Total variation is a way of measuring how much a function \(f:[a,b] \to \mathbb{R}\) “wiggles”. In this post, I want to motivate the definition of total variation by talking about elevation in marathon running. Comparing marathon courses…
-
Finding Australia’s youngest electorates with R
My partner recently wrote an article for Changing Times, a grassroots newspaper that focuses on social change. Her article, Who’s not voting? Engaging with First Nations voters and young voters, is about voter turn-out in Australia and an…
-
A clock is a one-dimensional subgroup of the torus
Recently, my partner and I installed a clock in our home. The clock previously belonged to my grandparents and we have owned it for a while. We hadn’t put it up earlier because the original clock movement…
-
Sampling from the non-central chi-squared distribution
The non-central chi-squared distribution is a generalisation of the regular chi-squared distribution. The chi-squared distribution turns up in many statistical tests as the (approximate) distribution of a test statistic under the null hypothesis. Under alternative hypotheses, those…
-
Non-measurable sets, cardinality and the axiom of choice
The following post is based on a talk I gave at the 2022 Stanford statistics retreat. The talk was titled “Another non-measurable monster”. The material was based on the discussion and references given in this stackexchange post.…
-
The Singular Value Decomposition (SVD)
The singular value decomposition (SVD) is a powerful matrix decomposition. It is used all the time in statistics and numerical linear algebra. The SVD is at the heart of the principal component analysis, it demonstrates what’s going…
-
Double cosets and contingency tables

Like my previous post, this blog is also motivated by a comment by Professor Persi Diaconis in his recent Stanford probability seminar. The seminar was about a way of “collapsing” a random walk on a group to…
-
The field with one element in a probability seminar
Something very exciting this afternoon. Professor Persi Diaconis was presenting at the Stanford probability seminar and the field with one element made an appearance. The talk was about joint work with Mackenzie Simper and Arun Ram. They…
-
Working with ABC Radio’s API in R
This post is about using ABC Radio’s API to create a record of all the songs played on Triple J in a given time period. An API (application programming interface) is a connection between two computer programs.…
-
Maximum likelihood estimation and the method of moments
Maximum likelihood and the method of moments are two ways to estimate parameters from data. In general, the two methods can differ but for one-dimensional exponential families they produce the same estimates. Suppose that \(\{P_\theta\}_{\theta \in \Omega}\)…
-
A not so simple conditional expectation
It is winter 2022 and my PhD cohort has moved on the second quarter of our first year statistics courses. This means we’ll be learning about generalised linear models in our applied course, asymptotic statistics in our…
-
Sports climbing at the 2020 Olympics
Last year sports climbing made its Olympic debut. My partner Claire is an avid climber and we watched some of the competition together. The method of ranking the competitors had some surprising consequences which are the subject…
-
Visualising Strava data with R
I’ve recently had some fun downloading and displaying my running data from Strava. I’ve been tracking my runs on Strava for the last five years and I thought it would be interesting to make a map showing…
-
Extremal couplings
This post is inspired by an assignment question I had to answer for STATS 310A – a probability course at Stanford for first year students in the statistics PhD program. In the question we had to derive…
-
You could have proved the Neyman-Pearson lemma
The Neyman-Pearson lemma is foundational and important result in the theory of hypothesis testing. When presented in class the proof seemed magical and I had no idea where the ideas came from. I even drew a face…
-
An art and maths collaboration
Over the course of the past year I have had the pleasure to work with the artist Sanne Carroll on her honours project at the Australian National University. I was one of two mathematics students that collaborated…
-
Leverages Scores
I am very excited to be writing a blog post again – it has been nearly a year! This post marks a new era for the blog. In September I started a statistics PhD at Stanford University.…
-
Commuting in Groups
In July 2020 I submitted my honours thesis which was titled “Commuting in Groups” and supervised by Professor Anthony Licata. You can read the abstract below and the full thesis here. Abstract In this thesis, we study…
-
Sums of Squares – Part 2: Motzkin
In the previous blog post we observed that if a polynomial \(g\) could be written as a sum \(\sum_{i=1}^n h_i^2\) where each \(h_i\) is a polynomial, then \(g\) must be non-negative. We then asked if the converse…
-
Sums of Squares – Part 1: Optimization
About a year ago I had the pleasure of having a number of conversations with Abhishek Bhardwaj about the area of mathematics his PhD is on. This pair of posts is based on the fond memories I…
-
Finitely Additive Measures
I am again tutoring the course MATH3029. The content is largely the same but the name has changed from “Probability Modelling and Applications” to “Probability Theory and Applications” to better reflect the material taught. There was a…
-
Why is the fundamental theorem of arithmetic a theorem?
The fundamental theorem of arithmetic states that every natural number can be factorized uniquely as a product of prime numbers. The word “uniquely” here means unique up to rearranging. The theorem means that if you and I…
-
Cayley Graphs and Cakes
Over the past month I have been studying at the AMSI Summer School at La Trobe University in Melbourne. Eight courses are offered at the AMSI Summer School and I took the one on geometric group theory.…
-
A Nifty Proof of the Cauchy-Schwarz Inequality
This blog post is entirely based on the start of this blog post by Terry Tao. I highly recommend reading the post. It gives an interesting insight into how Terry sometimes thinks about proving inequalities. He also…
-
The Outer Automorphism of S6
This blog post is about why the number 6 is my favourite number – because the symmetric group on six elements is the only finite permutation group that contains an outer automorphism. In the post we will…
-
Polynomial Pairing Functions
One of the great results of the 19th century German mathematician Georg Cantor is that the sets \(\mathbb{N}\) and \(\mathbb{N} \times \mathbb{N}\) have the same cardinality. That is the set of all non-negative integers \(\mathbb{N} = \{0,1,2,3,\ldots\}\)…
-
The Stone-Čech Compactification – Part 3
In the first blog post of this series we discussed two compactifications of \(\mathbb{R}\). We had the circle \(S^1\) and the interval \([-1,1]\). In the second post of this series we saw that there is a correspondence…
-
The Stone-Čech Compactification – Part 2
This is the second post in a series about the Stone-Čech compactification. In the previous post we discussed compactifications and defined the Stone-Čech compactification. In this blog post we will show the existence of the Stone-Čech compactification…
-
The Stone-Čech Compactification – Part 1
Mathematics is full of surprising connections between two seemingly unrelated topics. It’s one of the things I like most about maths. Over the next few blog posts I hope to explain one such connection which I’ve been…
-
Facebook and Graph Theory
Earlier this week I spoke at Maths and Computer Science in the Pub. The event was hosted by Phil Dooley and sponsored by the Mathematical Sciences Institute. I had a great time talking and hearing from the…
-
A minimal counterexample in probability theory
Last semester I tutored the course Probability Modelling with Applications. In this course the main objects of study are probability spaces. A probability space is a triple \((\Omega, \mathcal{F}, \mathbb{P})\) where: \(\Omega\) is a set. \(\mathcal{F}\) is…
-
[Link Post] Complexity Penalties in Statistical Machine Learning
Earlier in the year I wrote a post on Less Wrong about some of the material I learnt at the 2019 AMSI Summer School. You can read it here. On a related note, applications are open for…
-
Combing groups
Two weeks ago I gave talk titled “Two Combings of \(\mathbb{Z}^2\)”. The talk was about some material I have been discussing lately with my honours supervisor. The talk went well and I thought it would be worth…