Bernoulli’s inequality and probability

Suppose we have independent events \(E_1,E_2,\ldots,E_m\), each of which occur with probability \(1-\varepsilon\). The event that all of the \(E_i\) occur is \(E = \bigcap_{i=1}^m E_i\). By using independence we can calculate the probability of \(E\),

\(P(E) = P\left(\bigcap_{i=1}^m E_i\right) = \prod_{i=1}^m P(E_i) = (1-\varepsilon)^m.\)

We could also get a lower bound on \(P(E)\) by using the union bound. This gives,

\(P(E) = 1-P(E^c) = 1-P\left(\bigcup_{i=1}^m E_i^c\right) \ge `1-\sum_{i=1}^m P(E_i^c) = 1-m\varepsilon.\)

We can therefore conclude that \((1-\varepsilon)^m \ge 1-m\varepsilon\). This is an instance of Bernoulli’s inequality. More generally, Bernoulli’s inequality states that

\((1+x)^m \ge 1+mx,\)

for all \(x \ge -1\) and \(m \ge 1\). This inequality states the red line is always underneath the black curve in the below picture. For an interactive version of this graph where you can change the value of \(m\), click here.

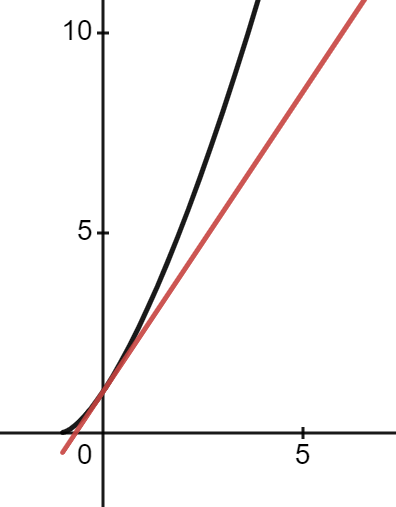
Our probabilistic proof only applies to that case when \(x = -\varepsilon\) is between \(-1\) and \(0\) and \(m\) is an integer. The more general result can be proved by using convexity. For \(m \ge 1\), the function \(f(x) = (1+x)^m\) is convex on the set \(x > -1\). The function \(g(x) = 1+mx\) is the tangent line of this function at the point \(x=0\). Convexity of \(f(x)\) means that the graph of \(f(x)\) is always above the tangent line \(g(x)\). This tells us that \((1+x)^m \ge 1+mx\).

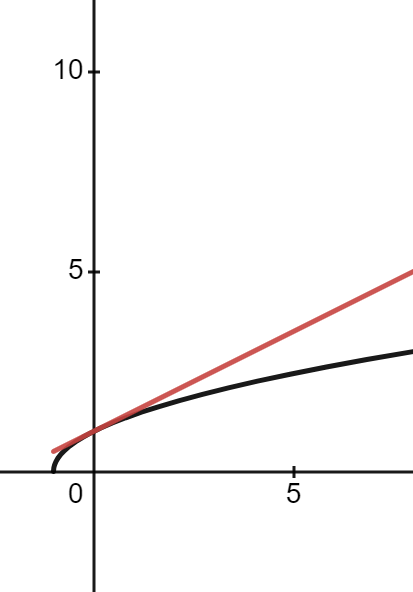
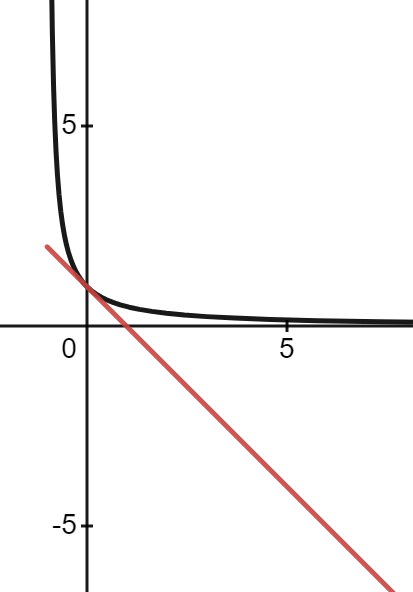
For \(m\) between \(0\) and \(1\), the function \((1+x)^m\) is no longer convex but actually concave and the inequality reverses. For \(m \le 0\), \((1+x)^m\) becomes concave again. These two cases are visualized below. In the first picture \(m = 0.5\) and the red line is above the black one. In the second picture \(m = -1\) and the black line is back on top.